|
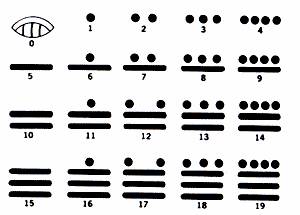
В Древнем Вавилоне примерно за 40 веков до нашего времени создалась по-местная (позиционная) нумерация, т.е. такой способ изображения чисел, при котором одна и та же цифра может обозначать разные числа в зависимости от места, занимаемого этой цифрой. Наша современная нумерация тоже поместная: в числе 52 цифра 5 обозначает пятьдесят, т.е.5х10, а в числе 576 эта же цифра обозначаёт пятьсот, т.е. 5х10х10. В вавилонской поместной нумерации ту роль, которую играет у нас число 10, играло число 60, и потому эту нумерацию называют шестидеситеричной. Числа, меньшие 60, обозначались с помощью двух знаков. Они имели клинообразный вид, так как вавилоняне писали на глиняных дощечках палочками треугольной формы. Эти знаки повторялись нужное число раз.
Шестидесятеричная система возникла позднее десятичной, ибо числа до 60 записываются в ней по десятичному принципу. Но до сих пор неизвестно, когда и как возникла у вавилонян шестидесятеричная система. На этот счет строилось много гипотез, но ни одна пока не доказана. Мнения историков по поводу того, как именно возникла эта система счисления, расходятся. Существуют две гипотезы. Первая исходит из того, что произошло слияние двух племен, одно из которых пользовалось шестеричной, другое — десятичной. Шестидесятеричная система счисления в данном случае могла возникнуть в результате своеобразного политического компромисса. Суть второй гипотезы в том, что древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60.
Шестидесятеричная запись целых чисел не получила распространения за пределами ассиро-вавилонского царства, но шестидесятеричные дроби проникли далеко за эти пределы: в страны Ближнего Востока, Средней Азии, в Северную Африку и Западную Европу. Они широко применялись, особенно в астрономии, вплоть до изобретения десятичных дробей, т.е. до начала XVII в.
3.2 Римская пятеричная

Это, наверное, самая известная система, после «арабской», она возникла более двух с половиной тысяч лет назад в Древнем Риме.
|
I |
1 |
|
V |
5 |
|
X |
10 |
|
L |
50 |
|
C |
100 |
|
D |
500 |
|
M |
1 000 |
Предполагаемое происхождение римских цифр

Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Например, XI = 11, XII = 12, XIII = 13, но следующее число уже особенное, так как такое число «XIIII» писать не удобно, римляне придумали сокращения, они стали писать так XIV = 14, т.е. 10+5-1 = 14. Т.е. если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание. Так же записывалось число 9 = IX. И кроме этого нельзя было писать четыре одинаковые цифры подряд, например, «XXXX» = XL (50-10) = 40.
О происхождении римских цифр достоверных сведений нет. В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян ни каких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (скорее всего этрусков). Такая нумерация преобладала в Италии до XIII века, а в других странах Западной Европы - до XVI века.
В Санкт- Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число: MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782 год. Это год открытия памятника.
Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д.
3.3 Древнегреческая аттическая пятеричная
В древнейшее время в Греции была распространена так называемая Аттическая система счисления, название происходит от области Греции – Аттики со столицей Афины.
В этой системе числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок:  , ,  , ,  , ,  . Число 5 записывалось знаком . Число 5 записывалось знаком  (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков: (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:

Число 10 обозначалось  - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно: - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно:

Числа в пределах первого десятка тысяч записывались так:

3.4 Древнегреческая ионийская десятеричная алфавитная
Примерно в третьем веке до нашей эры аттическая система счисления в Греции была вытеснена другой, так называемой "Ионийской" системой (она возникла в Милеете – греческая малоазиатская колония Ионии). В ней числа 1 - 9 обозначаются первыми буквами древнегреческого алфавита:

числа 10, 20, … 90 изображались следующими девятью буквами:

числа 100, 200, … 900 последними девятью буквами:

Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка '. Любая буква с этим значком сразу же становилась в тысячу раз больше.
Для отличия цифр и букв писали черточки над цифрами.

Древние евреи, арабы и многие другие народы Ближнего Востока имели такие же системы счисления.
При ее помощи можно было просто записать числа до ста миллионов (100 000 000). Эта система по быстроте счета мало отличается от «арабской». И хоть она не позиционная, но в ней есть мультипликативность.
3.5 Славянская глаголическая десятеричная
Эта система была создана для обозначения чисел в священных книгах западных славян. Использовалась она нечасто, но достаточно долго. По организации она в точности повторяет греческую нумерацию. Использовалась она с VIII по XIII в.
|
 1 1
|
 10 10
|
 100 100
|
 1 000 1 000
|
|
 2 2
|
 20 20
|
 200 200
|
|
|
 3 3
|
 30 30
|
 300 300
|
|
|
 4 4
|
 40 40
|
 400 400
|
|
|
 5 5
|
 50 50
|
 500 500
|
|
|
 6 6
|
 60 60
|
 600 600
|
|
|
 7 7
|
 70 70
|
 700 700
|
|
|
 8 8
|
 80 80
|
 800 800
|
|
|
 9 9
|
 90 90
|
 900 900
|
|
Числа записывали из цифр так же слева, направо, от больших к меньшим цифрам. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали. Такая запись числа аддитивная, то есть в ней используется только сложение:
   = 800+60+3 = 863 = 800+60+3 = 863
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, или точки.
3.6 Славянская кириллическая десятеричная алфавитная
Эта нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

Числа записывали из цифр так же слева, направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком:

Читаем дословно "четырнадцать" - "четыре и десять". Как слышим, так и пишем: не 10+4, а 4+10, - четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.
Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение:
 = 800+60+3 = 800+60+3
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке.
Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:
|

|
Тысяча |
1000 |
|

|
Тьма |
10 000 |
|

|
Легион |
100 000 |
|

|
Леодр |
1 000 000 |
|

|
Ворон |
10 000 000 |
|

|
Колода |
100 000 000 |
Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.
3.7 Древнеиндийские системы счисления
Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево.

Наряду с этой системой существовала в Индии еще одна система счисления брахми.

Числа брахми записывались слева направо. Однако в обеих системах было не мало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр брахми, было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр брахми в дальнейшем была использована при создании в Индии позиционной десятичной системы.
В древней Индии так же была словесная система счисления. Она была мультипликативная, позиционная. Знак нуля произносился как «пустое», или «небо», или «дыра». Единица как «луна», или «земля». Двойка как «близнецы», или «глаза», или «ноздри», или «губы». Четыре как «океаны», «стороны света». Например, число 2441 произносилось так: глаза океанов стороны света луны.
| 


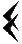 ,
,  ,
,  ,
,  . Число 5 записывалось знаком
. Число 5 записывалось знаком 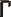 (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:
(древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:
 - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно:
- заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно:



































 = 800+60+3
= 800+60+3






