Интуитивное представление о числе, по-видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. То, что первобытные люди сначала знали только "один", "два" и "много", подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово "три" использовалось только в сочетаниях "три дерева" или "три человека"; представление о том, что эти множества имеют между собой нечто общее — понятие троичности — требует высокой степени абстракции. О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова "один" и "первый", равно как "два" и "второй", во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета "один", "два", "много", слова "три" и "третий", "четыре" и "четвертый" ясно указывают на взаимосвязь между количественными и порядковыми числительными.
Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по-видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.
Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово "двадцать три" — не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий "два раза по десять и три". Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах. По той же причине использовались основания пять или двадцать. На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерения или вычислений использовались основания 12 ? 60.
Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа. Для кочевых племен характерны устные названия чисел, что же касается письменных, то необходимость в них появилась лишь с переходом к оседлому образу жизни, образованием земледельческих сообществ. Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.
История наших привычных «арабских» чисел очень запутана. Нельзя сказать точно и достоверно как они произошли. Вот один из вариантов этого истории этого происхождения. Одно точно известно, что именно благодаря древним астрономам, а именно их точным расчетам мы и имеем наши числа.
Дроби. Вычисления с дробями включают сложение, вычитание, умножение и деление, а также упрощение сложных дробей.
Сложение дробей с одним и тем же знаменателем производится путем сложения числителей, например,
1/16 + 5/16 + 7/16 = (1 + 5 + 7)/16 = 13/16.
Если дроби имеют различные знаменатели, то предварительно их необходимо привести к общему знаменателю, т.е. превратить в дроби с одинаковыми знаменателями. Для этого мы находим наименьший общий знаменатель (наименьшее число, кратное каждому из данных знаменателей). Например, при сложении 2/3, 1/6 и 3/5 наименьший общий знаменатель равен 30:
Суммируя, получаем
20/30 + 5/30 + 18/30 = 43/30.
Вычитание дробей производится так же, как их сложение. Если знаменатели одинаковы, то вычитание сводится к вычитанию числителей: 10/13 – 2/13 = 8/13; если дроби имеют различные знаменатели, то предварительно необходимо привести их к общему знаменателю:
7/8 – 3/4 = 7/8 – 6/8 = (7 – 6)/8 = 1/8.
При умножении дробей их числители и знаменатели умножаются отдельно. Например,
5/6?4/9 = 20/54 = 10/27.
Чтобы разделить одну дробь на другую, необходимо умножить первую дробь (делимое) на дробь, обратную второй (делителю) (чтобы получить обратную дробь, надо поменять местами числитель и знаменатель исходной дроби), т.е. (n1/d1)?(n2/d2) = (n1?d2)/(d1?n2). Например,
3/4?7/8 = 3/4?8/7 = 24/28 = 6/7.
Смешанное число представляет собой сумму (или разность) целого числа и дроби, например, 4 + 2/3 или 10 – 1/8. Так как целое число можно рассматривать как дробь с знаменателем, равным 1, смешанное число есть не что иное, как сумма (или разность) двух дробей. Например,
4 + 2/3 = 4/1 + 2/3 = 12/3 + 2/3 = 14/3.
Сложной называется дробь, имеющая дробь либо в числителе, либо в знаменателе, либо в числителе и знаменателе. Такую дробь можно превратить в простую:
Квадратный корень. Если n – положительное действительное число, то существует единственное положительное действительное число r, такое, что r2 = n. Число r называется квадратным корнем из n и обозначается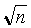 
. В школе учат извлекать квадратные корни двумя способами. Первый способ более популярен, поскольку он проще и его легче применять; вычисления по этому методу легко реализуются на настольном калькуляторе и обобщаются на случай кубических корней и корней более высокой степени. Основан метод на том, что если r1 – приближение к корню 
, то r2 = (1/2)(r1 + n/r1) – более точная аппроксимация корня.
Проиллюстрируем процедуру на примере вычисления квадратного корня из какого-нибудь числа, заключенного между 1 и 100, скажем, числа 40. Так как 62 = 36, а 72 = 49, мы заключаем, что 6 – наилучшее приближение к 
в целых числах. Более точное приближение к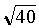 
получается из 6 следующим образом. Разделив 40 на 6, получим 6,6 (с округлением до первого после запятой четного числа десятых). Чтобы получить второе приближение к 
, усредним два числа 6 и 6,6 и получим 6,3. Повторив процедуру, получим еще лучшее приближение. Разделив 40 на 6,3, находим число 6,350, и третье приближение оказывается равным (1/2)(6,3 + 6,350) = 6,325. Еще одно повторение дает 40? 6,325 = 6,3241106, и четвертая аппроксимация оказывается равной (1/2)(6,325 + 6,3241106) = 6,3245553. Процесс может продолжаться сколь угодно долго. В общем случае каждое следующее приближение может содержать вдвое больше цифр, чем предыдущее. Так, в нашем примере, поскольку первое приближение, целое число 6, содержит только одну цифру, мы можем удерживать во втором приближении два знака, в третьем – четыре и в четвертом – восемь.
Если число n не лежит между 1 и 100, то следует предварительно разделить (или умножить) n на некоторую степень числа 100, скажем, на k-ю, чтобы произведение оказалось в интервале от 1 до 100. Тогда квадратный корень из произведения будет находиться в интервале от 1 до 10, и после того, как он будет извлечен, мы, умножив (или разделив) полученное число на 10k, найдем искомый квадратный корень. Например, если n = 400000, то мы сначала делим 400000 на 1002 и получаем число 40, лежащее в интервале от 1 до 100. Как показано выше, 
приближенно равен 6,3245553. Умножая это число на 102, получаем 632,45553 в качестве приближенного значения для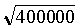 
, а число 0,63245553 служит приближенным значением для 
.
Вторая из упомянутых выше процедур основана на алгебраическом тождестве (a + b)2 = a2 + (2a + b)b. На каждом шаге уже полученная часть квадратного корня принимается за a, а часть, которую еще требуется определить, – за b.
Кубический корень. Для извлечения кубического корня из положительного действительного числа существуют алгоритмы, аналогичные алгоритмам извлечения квадратного корня. Например, чтобы найти кубический корень из числа n, сначала мы аппроксимируем корень некоторым числом r1. Затем строим более точное приближение r2 = (1/3)(2r1 + n/r12), которое в свою очередь уступает место еще более точному приближению r3 = (1/3)(2r2 + n/r22) и т.д. Процедура построения все более точных приближений корня может продолжаться сколь угодно долго.
Рассмотрим, например, вычисление кубического корня из числа, заключенного между 1 и 1000, скажем, числа 200. Так как 53 = 125 и 63 = 216, мы заключаем, что 6 – ближайшее к кубическому корню из 200 целое число. Следовательно, выбираем r1 = 6 и последовательно вычисляем r2 = 5,9, r3 = 5,85, r4 = 5,8480. В каждом приближении, начиная с третьего, разрешается удерживать число знаков, которое на единицу меньше удвоенного числа знаков в предыдущем приближении. Если же число, из которого требуется извлечь кубический корень, не заключено между 1 и 1000, то предварительно его необходимо разделить (или умножить) на некоторую, скажем, k-ю, степень числа 1000 и тем самым привести в нужный интервал чисел. Кубический корень из вновь полученного числа лежит в интервале от 1 до 10. После того, как он будет вычислен, его необходимо умножить (или разделить) на 10k , чтобы получить кубический корень из исходного числа.
Второй, более сложный, алгоритм нахождения кубического корня из положительного действительного числа основан на использовании алгебраического тождества (a + b)3 = a3 + (3a2 + 3ab + b2)b. В настоящее время алгоритмы извлечения кубических корней, равно как и корней более высоких степеней, в средней школе не изучают, так как их легче находить с помощью логарифмов или алгебраическими методами.
Алгоритм Евклида. Этот алгоритм был изложен в Началах Евклида (ок. 300 до н.э.). С его помощью вычисляется наибольший общий делитель двух целых чисел. Для случая положительных чисел он формулируется в виде процедурного правила: «Разделите большее из двух данных чисел на меньшее. Затем разделите делитель на остаток от деления и продолжайте действовать так же, пока последний делитель не разделится нацело на последний остаток. Последний из делителей и будет наибольшим общим делителем двух данных чисел».
В качестве числового примера рассмотрим два целых числа 3132 и 7200. Алгоритм в этом случае сводится к следующим действиям:
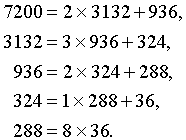
Наибольший общий делитель совпадает с последним делителем – числом 36. Объяснение просто. В нашем примере мы видим из последней строки, что число 36 делит число 288. Из предпоследней строки следует, что число 36 делит 324. Так, двигаясь от строки к строке вверх, мы убеждаемся в том, что число 36 делит 936, 3132 и 7200. Мы утверждаем теперь, что число 36 есть общий делитель чисел 3132 и 7200. Пусть g – наибольший общий делитель чисел 3132 и 7200. Так как g делит 3132 и 7200, из первой строки следует, что g делит 936. Из второй строки мы заключаем, что g делит 324. Так, спускаясь от строки к строке, мы убеждаемся в том, что g делит 288 и 36. А так как 36 – общий делитель чисел 3132 и 7200 и делится на наибольший общий их делитель, мы заключаем, что 36 и есть этот наибольший общий делитель.
Арабская система счисления
Как мы уже знаем, в вавилонской системе счисления присутствует знак для обозначения пропущенных разрядов. Примерно во II веке до н.э. с астрономическими наблюдениями вавилонян познакомились греческие астрономы (например, Клавдий Птолемей). Они переняли их позиционную систему счисления, но целые числа они записывали не с помощью клиньев, а в своей алфавитной нумерации, а дроби в вавилонской шестидесятеричной системой счисления. Но для обозначения нулевого значения разряда греческие астрономы стали использовать символ "0" (первая буква греческого слова Ouden - ничто).
Между II и VI веками н.э. индийские астрономы познакомились с греческой астрономией. Они переняли шестидесятеричную систему и круглый греческий нуль. Индийцы соединили принципы греческой нумерации с десятичной мультипликативной системой взятой из Китая. Так же они стали обозначать цифры одним знаком, как было принято в древнеиндийской нумерации брахми. Это и был завершающий шаг в создании позиционной десятичной системы счисления.
Блестящая работа индийских математиков была воспринята арабскими математиками и Аль-Хорезми в IX веке написал книгу "Индийское искусство счета", в которой описывает десятичную позиционную систему счисления. Простые и удобные правила сложения и вычитания сколь угодно больших чисел, записанных в позиционной системе, сделали ее особенно популярной в среде европейских купцов.
В XII в. Хуан из Севильи перевел на латынь книгу "Индийское искусство счета", и индийская система счета широко распространилась по всей Европе. А так как труд Аль-Хорезми был написан арабском языке, то за индийской нумерацией в Европе закрепилось неправильное название - "арабская". Но сами арабы именуют цифры индийскими, а арифметику, основанную на десятичной системе - индийским счетом.
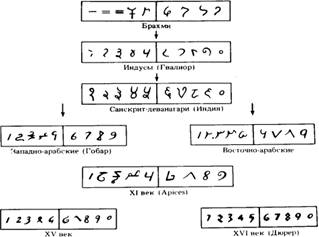
Форма «арабских» цифр со временем сильно изменялась. Та форма, в которой мы их пишем, установилась в XVI веке.
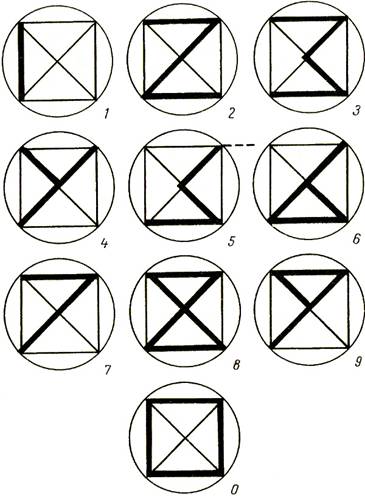
Даже Александр Сергеевич Пушкин предложил свой вариант формы арабских чисел. Он решил, что все десять арабских цифр, включая нуль, помещаются в магическом квадрате.
История нуля
Нуль бывает разный. Во-первых, нуль – это цифра, которая используется для обозначения пустого разряда; во-вторых, нуль – это необычное число, так как на нуль делить нельзя и при умножении на нуль любое число становиться нулем; в-третьих, нуль нужен для вычитания и сложения, иначе, сколько будет, если из 5 вычесть 5?
Впервые нуль появился в древневавилонской системе счисления, он использовался для обозначения пропущенных разрядов в числах, но такие числа как 1 и 60 у них записывали одинаково, так как нуль в конце числа у них не ставился. В их системе нуль выполнял роль пробела в тексте.
Изобретателем формы нуля можно считать великого греческого астронома Птолемея, так как в его текстах на месте знака пробела стоит греческая буква омикрон, очень напоминающая современный знак нуля. Но Птолемей использует нуль в том же смысле, что и вавилоняне.
На стенной надписи в Индии в IX веке н.э. впервые символ нуля встречается в конце числа. Это первое общепринятое обозначение современного знака нуля. Именно индийские математики изобрели нуль во всех его трех смыслах. Например, индийский математик Брахмагупта еще в VII века н.э. активно стал использовать отрицательные числа и действия с нулем. Но он утверждал, что число, деленное на нуль, есть нуль, что конечно ошибка, но настоящая математическая дерзость, которая привела к другому замечательному открытию индийских математиков. И в XII веке другой индийский математик Бхаскара делает еще попытку понять, что же будет при делении на нуль. Он пишет: "количество, деленное на нуль, становится дробью, знаменатель которой равен нулю. Эту дробь называют бесконечностью".
Леонардо Фибоначчи, в своем сочинении "Liber abaci" (1202) называет знак 0 по-арабски zephirum. Слово zephirum – это арабское слово as-sifr, которое произошло от индийского слова sunya, т. е. пустое, служившего названием нуля. От слова zephirum произошло французское слово zero (нуль) и итальянское слово zero. С другой стороны, от арабского слова as-sifr произошло русское слово цифра. Вплоть до середины XVII века это слово употреблялось специально для обозначения нуля. Латинское слово nullus (никакой) вошло в обиход для обозначения нуля в XVI веке.
Нуль - это уникальный знак. Нуль – это чисто абстрактное понятие, одно из величайших достижений человека. Его нет в природе окружающей нас. Без нуля можно спокойно обойтись в устном счете, но невозможно обойтись для точной записи чисел. Кроме этого, нуль находится в противовесе всем остальным числам, и символизирует собой бесконечный мир. И если “все есть число”, то ничто есть все!
