Цифры и системы счисления

  Зачем числа?

"Все есть число", — говорили пифагорийцы (ученики древнегреческого математика Пифагора). Значит всё можно обозначить числом.

Так как многие предметы внешнего мира имеет схожую форму, возникла потребность их сосчитать. Например, сколько коров в стаде. Сколько добыто рыб, или зайцев. Т.е. число и арифметика возникли из практической деятельности человека.

Так как многие народы в древности не общались друг другом, то у разных народов возникли разные системы счисления и представления чисел и цифр.

Число - это обобщение, так как разными числами можно подсчитать разные предметы.

Цифры – это значки, с помощью которых записывают числа. Система счисления или нумерация – это способ записи чисел с помощью цифр.

     Простая система счисления

У первобытных людей не было даже чисел, они количество предметов отображали равным количеством каких-либо значков. Такими значками могли быть зарубки, черточки, точки, а так же узелки на веревках.

 Это самая простая система счисления. В этой системе счисления для записи чисел используется только одна цифра. Ее можно изобразить в виде палочки ?, кружочка 0, или любой другой фигуры. Тогда числа будут записываться примерно так:

1	?
2	??
3	???
4	???
5	? ? ? ? ? и т. д.

Такая система счисления использовалась, и до сих пор используется народами, не имеющими письменности.

Но иногда такой системой счисления пользуются и современные люди, например, отмечая зарубками количество прошедших дней, или карандашом отмечая черточками в тетради количество проданных товаров.

Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.

Но это удобно, пока числа небольшие. Вы только представьте себе число 1 000 записанное с помощью кучки камушков, а 1 000 000? Неудобно?

И люди начали изобретать системы счисления.

 Позиционные и непозиционные системы счисления

Системы счисления бывают непозиционными (аддитивными) и позиционными (мультипликативными).

Чтобы разобраться в этом рассмотрим для примера нашу «арабскую» систему счисления. Например, число 3333 – три тысячи триста тридцать три. Здесь каждая цифра «3» в зависимости от того, в каком месте находиться обозначает свое число. Первая тройка слева, это три тысячи, вторая, три сотни, третья – три десятка, четвертая – три единицы. Т.е. это позиционная система. В таких же системах значение каждой цифры, зависит от ее положения (места, позиции) в записи числа. В непозиционных системах значение каждой цифры не зависит от ее положения (места, позиции) в записи числа.

Число 3333 можно представить в таком виде 3?1000 + 3?100 + 3?10 + 3. Т.е. для представления этого числа используется умножение (по-английски multiplication), отсюда название этой системы - мультипликативная.

В непозиционных же системах для представления числа используется сложение всех цифр, по-английски сложение – add. Поэтому другое название этих систем - аддитивные.

 Основание системы счисления

Основание системы счисления – это число, на основе которого ведется счет. Например, если основание системы счисления равно десяти, то минимальная счетная группа этой системы счисления равна десяти, это значит, что, сосчитав какие-либо предметы до десяти, мы считаем снова с единицы, но при этом запоминаем число десятков. В нашей «арабской» системе основанием является число десять. Есть системы счисления и с другим основанием. Это такие системы счисления как пятеричная, двенадцатеричная, двадцатеричная, шестидесятеричная.

Десятеричная и пятеричная система возникла от того факта, что на одной руке человека пять пальцев, на обоих руках 10 пальцев.

Так проще считать. Если добавить пальцы и на ногах, то будет понятная и двадцатеричная система. Происхождение двенадцатеричной системы тоже связано со счетом на пальцах. Считали большой палец руки и фаланги остальных четырех пальцев.

Если двенадцать умножить на пять получим шестидесятеричную систему. Например, на одной руке загибаем пальцы, пока не получим, что отсчитано, пять штук, а на другой руке прикосновением большого пальца к суставам остальных четырех указываем количество этих пятерок.

В некоторых системах счисления используются для обозначения цифр буквы, такие системы счисления называются алфавитными.

Итак, бывают непозиционные (аддитивные) и позиционные (мультипликативные), пятеричные, десятичные, двенадцатеричные, двадцатеричные, шестидесятеричные и алфавитные системы счисления.

Вначале рассмотрим непозиционные (аддитивные) системы счисления.

    Непозиционные системы счисления

     Древнеегипетская десятичная

Примерно  в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.

        Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной и аддитивной.

	1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки.
	Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем ряду должно быть столько же палочек, сколько и в верхнем, или на одну больше.
	10. Такими путами египтяне связывали коров
	Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.
	100. Это мерная веревка, которой измеряли земельные участки после разлива Нила.
	1 000. Вы когда-нибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка.
	10 000. "В больших числах будь внимателен!" - говорит поднятый вверх указательный палец.
	100 000. Это головастик. Обычный лягушачий головастик.
	1 000 000. Увидев такое число, обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф
	10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца

Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.

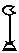
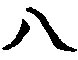
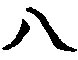
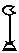
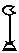
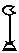
- 1205, - 1 023 029

Попробуйте сложить эти два числа, зная, что более 9 одинаковых иероглифов использовать нельзя, и вы сразу поймете, что для работы с этой системой нужен специальный человек. Обычному человеку это не под силу. 

   Недостатки непозиционной системы счисления

Непозиционные системы счисления имеют ряд существенных недостатков:

1.    Существует постоянная  потребность введения новых знаков для записи больших чисел.

2.    Невозможно представлять дробные и отрицательные числа.

3.    Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков был счетная доска абак – что-то наподобие наших счетов.

Но мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.

Далее рассмотрим позиционные системы счисления. 

   Позиционные системы счисления

    Вавилонская десятеричная / шестидесятеричная

В древнем Вавилоне примерно во II тысячелетие до нашей эры была такая система счисления - числа менее 60 обозначались с помощью двух знаков: для единицы, и для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например

- 3; - 20; - 32;  - 59

Числа больше 60 записывались по разрядам, с небольшими пробелами между ними:

Так записывается число 302, то есть 5*60+2.

1*60*60+2*60+5 = 3725

А это 1*60*60+2*60+5 = 3725.

Но представление не которых чисел в этой системе будет одинаковым, например, число 302, может быть и равно и 5*60*60 + 2 = 18002. Так как нет значка для обозначения нуля.

Лишь в V веке до нашей эры был введен особый знак 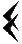 - наклонный клин для обозначения пропущенных разрядов, игравший роль нуля.

2*60*60+3 = 7203

это запись числа 7203 (2*60*60+3).

Однако отсутствие низшего разряда не обозначалось, и поэтому число 180 = 3*60 записывалось так , а обозначать эта запись могла и 3, и 180, и 10800 (3*60*60), и т. д.

Считается, что десятичная система была у шумеров, а после того как их завоевали семиты, их система была приспособлена под  шестидесятеричную систему семитов.

Шестидесятеричная запись целых чисел не получила широкого распространения за пределами Ассиро-вавилонского царства, но шестидесятеричные дроби применяются до сих пор при измерении времени. Например, одна минута = 60 секунд, один час = 60 минут.

     Древнекитайская десятеричная

Эта система одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную «арабскую», которой мы с Вами пользуемся. Возникла эта система около 4 000 тысяч лет тому назад в Китае.

	1		6
	2		7
	3		8
	4		9
	5	O	0

Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда - кружок - аналог нашего нуля). Чтобы не перепутать разряды использовали несколько служебных иероглифов, писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде.

10	100	1 000	10 000

- 1*1 000 = 1000;

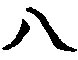  - 5 * 100+4* 10+8 = 548

Эта мультипликативная запись, так как в ней используется умножение. Она десятичная, в ней есть знак нуля, кроме этого она позиционная. Т.е. она почти соответствует «арабской» системе счисления.

   Двадцатеричная система счисления индейцев Майя или долгий счет

Эта система очень интересна тем, что на ее развитие не повлияла ни одна из цивилизаций Европы и Азии. Эта система применялась для календаря и астрономических наблюдений. Характерной особенностью ее было наличие нуля (изображение ракушки). Основанием этой системы было число 20, хотя сильно заметны следы пятеричной системы. Первые 19 чисел получались путем комбинирование точек (один) и черточек (пять).

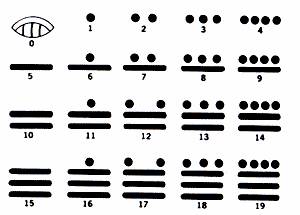
Число 20 изображалось из двух цифр, ноль и один наверху   и называлось уиналу. Записывались числа столбиком, внизу располагались наименьшие разряды, вверху наибольшие, в результате получалась «этажерка» с полками. Если число ноль появлялось без единицы наверху, то это обозначало, что единиц данного разряда нет. Но, если хоть одна единица была в этом разряде, то знак нуля исчезал, например, число 21, это будет . Так же в нашей системе счисления: 10 – с нулем, 11 – без него. Вот несколько примеров чисел:

В двадцатеричной системе счета древних майя есть исключение: стоит прибавить к числу 359 только одну единицу первого порядка, как это исключение немедленно вступает в силу. Суть его сводится к следующему: 360 является начальным числом третьего порядка и его место уже не на второй, а на третьей полке.

Но тогда выходит, что начальное число третьего порядка больше начального числа второго не в двадцать раз (20x20=400, а не 360!), а только в восемнадцать! Значит, принцип двадцатеричности нарушен! Все верно. Это и есть исключение.

Дело в том, что у индейцев Майя 20 дней-кинов образовывали месяц или уинал. 18 месяцев-уиналов образовывали год или туну (360 дней в году) и так далее:

        К'ин = 1 день.
        Виналь = 20 к'ин = 20 дней.
        Тун = 18 виналь = 360 дней = около 1 года.
        К'атун = 20 тун = 7200 дней = около 20 лет.
        Бак'тун = 20 к'атун = 144000 дней = около 400 лет.
        Пиктун = 20 бак'тун = 2880000 дней = около 8000 лет.
        Калабтун = 20 пиктун = 57 600 000 дней = около 160000 лет.
        К'инчильтун = 20 калабтун = 1152000000 дней = около 3200000 лет.
        Алавтун = 20 к'инчильтун = 23040000000 дней = около 64000000 лет.

Это довольно сложная система счисления, в основном использовалась жрецами для астрономических наблюдений, другая система индейцев Майя была аддитивной, похожей на египетскую и применялась в повседневной жизни.